This is a collection of basic information and techniques for using MATLAB. These involve both the "symbolic" (x is a variable without any particular value) and the "numerical" (x is a particular number or vector of numbers or matrix of numbers) functions of MATLAB.
Overview: Things to Know
a.
is pi and 
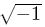is either i or j.b. MATLAB versions of common functions:
| Function | MATLAB | Example |
|---|---|---|
| xn | x^n |  |
| ex | exp(x) |  |
| ln x | log(x) |  |
| sinh x, cosh x | sinh(x), cosh(x) | sinh(1)  sinh(1) |
| sin x, cos x | sin(x), cos(x) | sin() sin(pi) |
| sin-1 x or arcsin x | asin(x) | arcsin 0.3 asin(0.3) |
 | sqrt(x) |  |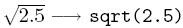
c. You can use the arrow keys
and 
keys to move back and forth through the list of past commands ("history"). If you bring back a previous command, you can change it (use the 
and keys to move to parts you want to delete or replace or add something) and rerun the commands (by pressing "Enter").d. Getting help: To find help for any function (e.g., exp), type help exp (or whatever the function is) at the >> command prompt. Or, bring up the "Help Browser" using F1 (or "MATLAB Help" under the "Help" menu in the main MATLAB window).
Using the Symbolic Toolkit
To use variables like x and y and a that are not assigned particular values (that is, we don�t say x = 1), we have to declare them as "symbolic". (Note: in Mathematica, the distinction is made internally and is not declared). We�ll do that here using syms. For example,
syms x y adelares the symbols x, y, and a, which we can then use to take derivatives, do Taylor expansions, etc. (see below).
a. Making simple plots.
To make a plot of a symbolic function, we can use ezplot. In the future, we�ll often use plot instead to generate graphs of numbers from our programs.
Example:
syms x ezplot(sin(x),[0,pi])will pop up a window with a plot of sin x with x ranging from 0 to
.b. Taking (symbolic) derivatives.
To take the derivative of e-ax2 (for example), declare a and x to be symbolic and then use the diff function:
syms a x diff(exp(-a*x^2)) To specify that x sin y should be differentiated with respectto y (with x held constant):
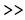syms x y 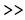diff(x*sin(y),y) (that is, the second argument is the differentiation variable).c. Doing Taylor expansions.
We can do Taylor expansions of symbolic functions. To expand eax in powers of x about x = 0 out to x4:
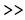syms a x 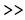taylor(exp(a*x),5,x,0)Note that we used 5 to get out to x4 (one more than the highest power we want). You
can make the result more readable by typing:
pretty(ans)after the taylor command (ans is the generic answer to the last command).
Scripts and Functions in MATLAB
Here we give some additional explanation of the my area.m script and the circle area.m function as examples. They are run by typing the name (without the .m ending) at the command prompt, e.g.,
my_area will run my area.m.a. % is used to mark a comment to help explain what the program is doing (or supposed to do!). Everything on a line after a % is ignored. Examples:
% This is a comment line only; no MATLAB instructions.
height = 5 % This comment might say that height is in meters
b. A semicolon ; is used at the end of a line to suppress extra output from MATLAB, which might be distracting.
c. input is used to get a value from the user for a variable. The general form is:
variable_name = input('message to be displayed')
For example,
radius = input('Enter the radius of a circle: ');
d. disp is used for output of a message (in the form of text enclosed in single quotes) or the value of a variable. For example,
disp('The area is: ')
disp(area)
e. A MATLAB function is like a script but it starts with a function declaration with a list of outputs between []'s, then an =, then the name of the function (same as the filename), then the list of inputs in ()'s. Example:
function [area] = circle_area (radius)
which takes radius as input and returns area.