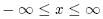
The unit vectors
, 
, and 
are also illustrated in Figure
These unit vectors are every where mutually orthogonal. The "del" operator in rectangular coordinates is simply:
The Laplacian operator in rectangular coordinates is :
Cylindrical Coordinates
The coordinate system is illustrated in Figure below. The location of a pointin three dimensional space may be specified by an ordered set of numbers(r,
, z). The ranges for the coordinate parameters are:
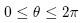
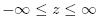
The relationship between rectangular and cylindrical coordinates is summarized as follows:
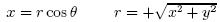
z = z z = z
The unit vectors
, 
, and 
are also illustrated in above figure. These unit vectors are every where mutually orthogonal. In contrast torectangular coordinates, the unit vectors 
and 
change direction dependingon the particular point in space. For this reason, it is critical to take care when executing diferential operations in cylindrical coordinates.For example,
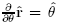and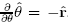 
. The "del" operator in cylindrical coordinates is:
The Laplacian operator in cylindrical coordinates is :
Spherical Coordinates
The coordinate system is illustrated in Figure below. The location of a pointin three dimensional space may be speci�ed by an ordered set of numbers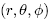
. The ranges for the coordinate parameters are:
Note carefully that the definitions of
are very diferent in the cylindricaland spherical coordinate systems! The relationship between rectangular and spherical coordinates is summarized as follows: |  |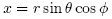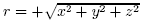
 |  |
 |  |
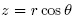The unit vectors
, 
and 
are also illustrated in Figure below.These unit vectors are every where mutually orthogonal. In contrast to rectangular coordinates, each of these unit vectors changes direction dependingon the particular point in space. For this reason, it is critical to take care when executing diferential operations in spherical coordinates.
For example,
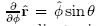and 
The "del" operator in spherical coordinates is:
The Laplacian operator in spherical coordinates is :
