Starting with:
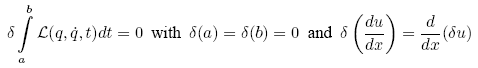
the equations of Lagrange can be derived:
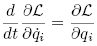
When there are additional conditions applying to the variational problem
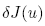 = 0 of the type K(u) =constant, the new problem becomes:
= 0 of the type K(u) =constant, the new problem becomes: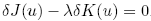
Hamilton mechanics
The Lagrangian is given by:
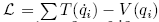 The Hamiltonian is given by:
The Hamiltonian is given by: 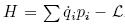
In 2 dimensions holds:
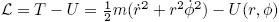 .
.If the used coordinates are canonical the Hamilton equations are the equations of motion for the system:
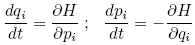
Coordinates are canonical if the following holds:
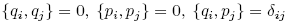 where {,} is the Poisson bracket:
where {,} is the Poisson bracket: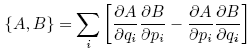
The Hamiltonian of a Harmonic oscillator is given by
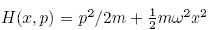 . With new coordinates
. With new coordinates  obtained by the canonical transformation
obtained by the canonical transformation 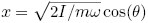 and
and 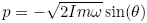 , with inverse
, with inverse 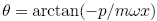 and
and 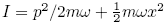 it follows:
it follows:  .
.The Hamiltonian of a charged particle with charge q in an external electromagnetic field is given by:
This Hamiltonian can be derived from the Hamiltonian of a free particle
 with the transformations
with the transformations  and
and 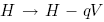 . This is elegant from a relativistic point of view: this is equivalent to the transformation of the momentum 4-vector
. This is elegant from a relativistic point of view: this is equivalent to the transformation of the momentum 4-vector 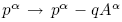 . A gauge transformation on the potentials
. A gauge transformation on the potentials 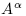 corresponds with a canonical transformation, which make the Hamilton equations the equations of motion for the system.
corresponds with a canonical transformation, which make the Hamilton equations the equations of motion for the system. Motion around an equilibrium, linearization
For natural systems around equilibrium the following equations are valid:
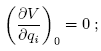
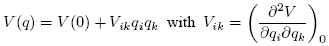
With
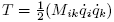 one receives the set of equations
one receives the set of equations 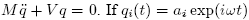 is substituted, this set of equations has solutions if
is substituted, this set of equations has solutions if 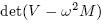 = 0.
= 0.This leads to the eigenfrequencies of the problem:
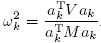
If the equilibrium is stable holds:
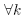 that
that 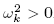 .
.The general solution is a superposition if eigenvibrations.
Phase space, Liouville's equation
In phase space holds:
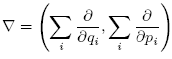
If the equation of continuity,
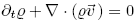 holds, this can be written as:
holds, this can be written as: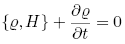
For an arbitrary quantity A holds:
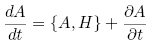
Liouville's theorem can than be written as:
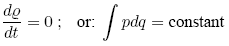
Generating functions
Starting with the coordinate transformation: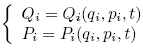
one can derive the following Hamilton equations with the new Hamiltonian K:
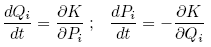
Now, a distinction between 4 cases can be made:
1.
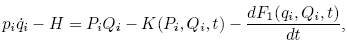 , the coordinates follow from:
, the coordinates follow from: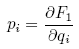 ;
; 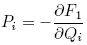 ;
; 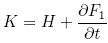
2.
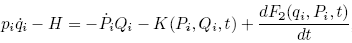 , the coordinates follow from:
, the coordinates follow from: ;
; 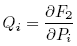 ;
; 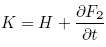
3.
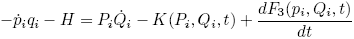 , the coordinates follow from:
, the coordinates follow from: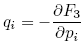 ;
; 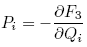 ;
; 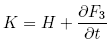
4.
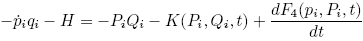 , the coordinates follow from:
, the coordinates follow from: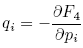 ;
; 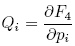 ;
; 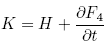
The functions F1, F2, F3 and F4 are called generating functions.